Méthodes numériques
-
Les méthodes de Runge-Kutta sont des méthodes d'analyse numérique d'approximation de solutions d'équations différentielles. Elles ont été nommées ainsi en l'honneur des mathématiciens Carl Runge et Martin Wilhelm Kutta lesquels élaborèrent la méthode en 1901.
- a)Représentation analytique de l'algorithme de Runge Kutta
- b)Paramètres de simulation
- c)Implémentation en C En mettant les équations obtenues précédemment, nous pouvons ensuite les résoudre à l'aide de notre programme et faire une étude de nos pendules.
Ces méthodes reposent sur le principe de l'itération, c'est-à-dire qu'une première estimation de la solution est utilisée pour calculer une seconde estimation, plus précise, et ainsi de suite.
On va utiliser ici le langage informatique C .La méthode de résolution de Runge-Kutta sera utilisée pour résoudre les différentes équations différentielles énumérées plus haut.
Nous utilisons ici le Runge-Kutta classique d'ordre 4, dénoté RK4 dans notre programme. La méthode RK4 est donnée par l'équation : - yn+1 = yn + h(k1 +2k2 +2k3 +k4 )/6
avec :
- k1 = y(xn ,fn )
- k2 = y(xn + h/2 ,yn + h/2 k1 )
- k3 = y(xn + h/2 ,yn + h/2 k2 )
- k4 = y(xn +h,yn +hk3 )
Nous nous servirons de notre programme afin de simuler les différents portraits de phase de notre pendule. Notre pendule incliné redevient un ependule simple dans les conditions :
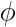 =
= -Déclaration des diverses constantes utilisées par la suite :
g :constante de pesanteur
l :longueur du pendule
-On initialise les différentes valeurs de
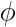 ,
, 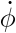 .
.-On fixe les paramètres dont principalement
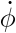 et l'énergie mécanique (Em=Ec+Ep).En effet lorsque l'on
se choisit un angle
et l'énergie mécanique (Em=Ec+Ep).En effet lorsque l'on
se choisit un angle 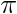 ) au temps t=0,cela donne à notre système une valeur d'énergie minimale(Ep).Et à cette énergie viendra s'ajouter celle acquise par le pendule du fait de la rotation du système
autour de l'axe z, par la vitesse angulaire
) au temps t=0,cela donne à notre système une valeur d'énergie minimale(Ep).Et à cette énergie viendra s'ajouter celle acquise par le pendule du fait de la rotation du système
autour de l'axe z, par la vitesse angulaire 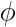 .De ce fait notre choix d'énergie mécanique ne doit pas être
inférieure au minimal de l'énergie du système qui aura été déterminé par les paramètres cités précédemment.
Cela entraneîrait un bug de la simulation(selon le type de machine utilisé).
.De ce fait notre choix d'énergie mécanique ne doit pas être
inférieure au minimal de l'énergie du système qui aura été déterminé par les paramètres cités précédemment.
Cela entraneîrait un bug de la simulation(selon le type de machine utilisé).